Dans cet article niveau terminale S, notre e-prof en ligne de soutien scolaire mathématiques vous propose un exercice associant géométrie et rugby.
Ce cours de soutien scolaire mathématiques en ligne ayant pour thème la transformation au rugby est proposé d’après un exercice de maths donné au Bac S en juin 2016 en Métropole.
Niveau : TS
Pré requis : Réaliser une figure de géométrie dynamique en respectant une échelle.
Placer un point libre sur un objet, visualiser la mesure d’un angle.
Trigonométrie. Etude d’une fonction.
Ce soir, c’est France-All Black au stade de France pour la finale de la coupe du monde 2023 de rugby. Nous sommes à la 78ème minute, la France vient de marquer un essai au point ![]() (voir figure ci-dessous) situé à l’extérieur du segment
(voir figure ci-dessous) situé à l’extérieur du segment ![]() , à 10 mètres à droite du poteau droit. Le score est à présent de 24 – 25 en faveur des Blacks. Un joueur Français doit transformer l’essai qui a été marqué.
, à 10 mètres à droite du poteau droit. Le score est à présent de 24 – 25 en faveur des Blacks. Un joueur Français doit transformer l’essai qui a été marqué.
 La transformation consiste à taper le ballon par un coup de pied depuis un point
La transformation consiste à taper le ballon par un coup de pied depuis un point ![]() que le joueur a le droit de choisir n’importe où sur le segment
que le joueur a le droit de choisir n’importe où sur le segment ![]() perpendiculaire à la droite
perpendiculaire à la droite ![]() sauf en
sauf en ![]() . La transformation est réussie si le ballon passe entre les poteaux repérés par les points
. La transformation est réussie si le ballon passe entre les poteaux repérés par les points ![]() et
et ![]() sur la figure.
sur la figure.
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point ![]() qui rend l’angle
qui rend l’angle ![]() le plus grand possible.
le plus grand possible.
Vous êtes ramasseur de balle, vous récupérer le ballon pour le donner au joueur avant sa transformation. En lui passant le ballon, vous lui susurrez : « Place-toi à 12,5 mètres de la ligne d’en-but ! Ton angle sera maximal ! »
Le joueur interloqué répond avec sourire : « Ah ouais, il vaut combien cet angle ? »
Soucieux de donner un coup de main à l’équipe de France, vous vous mettez au boulot.
Le but de cet exercice est donc de rechercher, si elle existe, la position du point ![]() sur le segment
sur le segment ![]() pour laquelle l’angle
pour laquelle l’angle ![]() est maximum et, si c’est le cas, de déterminer une valeur approchée de cet angle.
est maximum et, si c’est le cas, de déterminer une valeur approchée de cet angle.
Les dimensions du terrain sont les suivantes : ![]() = 50 m,
= 50 m, ![]() = 5,6 m et
= 5,6 m et ![]() = 10 m
= 10 m
1re méthode: Utilisation d’un logiciel de géométrie dynamique
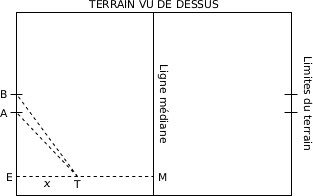
Construire à l’aide du logiciel GeoGebra une figure décrivant la moitié d’un terrain de rugby avec la ligne d’en-but, les poteaux, … (on prendra comme échelle 1 cm pour 2,5 m)
Sur l’axe des abscisses, placer ![]() et
et ![]() base des poteaux gauche et droit distants de 5,6 m, où
base des poteaux gauche et droit distants de 5,6 m, où ![]() a pour coordonnées
a pour coordonnées ![]() ;
;
E le point de la ligne d’en-but perpendiculaire à l’essai du joueur Français, situé à 10 m à droite de ![]() .
.
![]() situé sur la perpendiculaire à la ligne d’en-but à 50 m de celle-ci.
situé sur la perpendiculaire à la ligne d’en-but à 50 m de celle-ci.
![]() la position du joueur tentant la transformation, variable sur 50 m perpendiculairement à la ligne d’en-but.
la position du joueur tentant la transformation, variable sur 50 m perpendiculairement à la ligne d’en-but.
Afficher ensuite : la distance ![]() et la mesure de l’angle
et la mesure de l’angle ![]() .
.
En déplaçant le point T, retrouver le résultat susurré au joueur.
 Aide Prof Express : tracer le cercle circonscrit au triangle
Aide Prof Express : tracer le cercle circonscrit au triangle ![]() et noter
et noter ![]() son centre.
son centre.
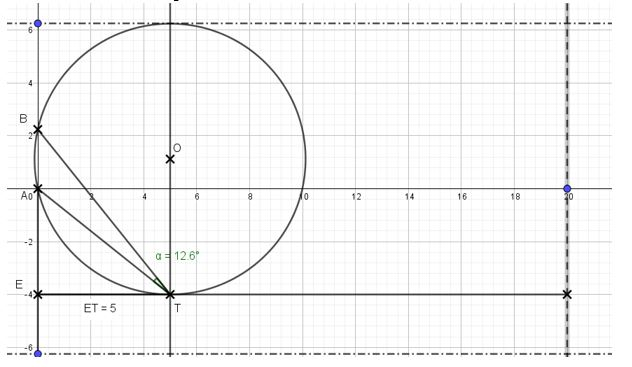
Vous devez constater que la position optimale de ![]() correspond au cas où le cercle circonscrit au triangle
correspond au cas où le cercle circonscrit au triangle ![]() est tangent à la perpendiculaire à
est tangent à la perpendiculaire à ![]() passant par
passant par ![]() , c’est-à-dire que la droite
, c’est-à-dire que la droite ![]() est parallèle à
est parallèle à ![]() .
.
Vous devez obtenir une figure ressemblant à celle-ci.
Le fichier est téléchargeable par ce lien !
2e méthode: Etude d’une fonction numérique
Dans toute la suite, on note ![]() la longueur
la longueur ![]() , que l’on cherche à déterminer.
, que l’on cherche à déterminer.
On note ![]() la mesure en radian de l’angle
la mesure en radian de l’angle ![]() ,
, ![]() la mesure en radian de l’angle
la mesure en radian de l’angle ![]() et
et ![]() la mesure en radian de l’angle
la mesure en radian de l’angle ![]() .
.
Dans le triangle ![]() rectangle en
rectangle en ![]() , en utilisant les relations trigonométriques élémentaires nous avons :
, en utilisant les relations trigonométriques élémentaires nous avons : ![]()
De même en travaillant dans le triangle ![]() rectangle en
rectangle en ![]()
nous avons: ![]()
On admet que pour tous réels ![]() et
et ![]() de l’intervalle
de l’intervalle ![]()
![]()
Nous avons : ![]() et il s’ensuit que :
et il s’ensuit que :
![]()
![]()
![]()
![]()
![]()
On va étudier la fonction définie par :
![]()
La fonction f est dérivable sur ![]()
![]()
![]()
![]()
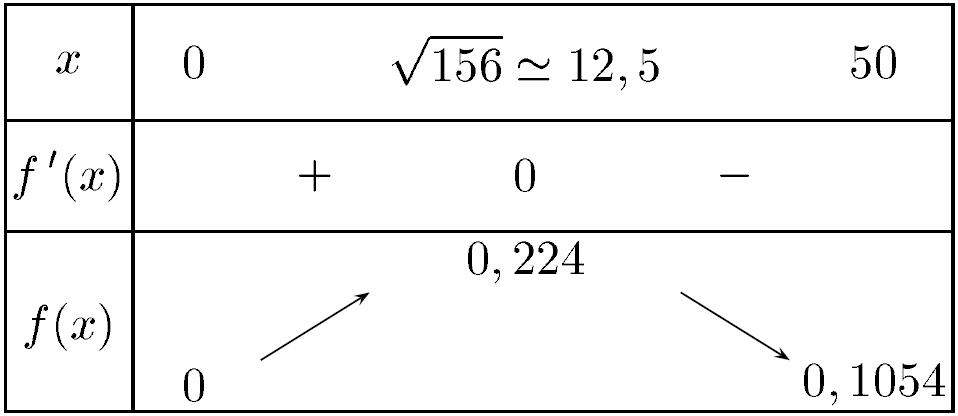 On obtient donc le tableau de variation suivant :
On obtient donc le tableau de variation suivant :
On constate que ![]() admet un maximum pour
admet un maximum pour ![]()
On a alors ![]() soit
soit ![]()
Conclusion : L’angle maximal est de 12,6°, il est obtenu lorsque la transformation a lieu à 12,5 m de l’en-but.
[/av_textblock]
Cliquer ici pour ajouter votre propre texte
Retrouvez nos nombreux articles de révision et préparation bac mathématiques dans notre blog de soutien scolaire en ligne.






Répondre
Want to join the discussion?Feel free to contribute!