Révisons ce cours de mathématiques en ligne niveau lycée (terminale) sur les graphes et les matrices avec un exercice sur la météo.
Fera-t-il beau demain?
En route pour le Bac : Graphes et Météo.
Niveau : TES (Spécialité) – TS (Spécialité).
Connaissances requises : Graphes Probabilistes – Matrices.
Énoncé et correction :
Dans une région, on note 
l’état “il fait beau” et 
l’état “Il ne fait pas beau”.
Si il fait beau un jour, la probabilité qu’il refasse beau le lendemain est de 
.
Si il ne fait pas beau un jour, la probabilité qu’il ne refasse pas beau le lendemain est de 
.
Aujourd’hui il fait beau.
Représentons ces données par un graphe probabiliste 
de sommet et , et déterminons sa matrice de transition 
.
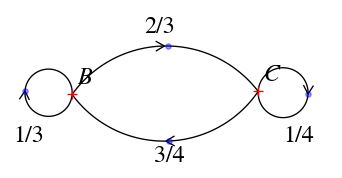
Graphe :
Matrice de Transition:
Pour un entier naturel 
donné, on note 
la matrice ligne décrivant l’état probabiliste lors de la journée .
Il fait beau aujourd’hui, l’état probabiliste initial est donc 
.
Déterminons la probabilité qu’il fasse beau le 7e jour.
On a 
où 
est l’état initial.
et ainsi de suite.
On a donc : 
A la calculatrice on trouve : 
Donc il y a environ 53% de chance qu’il fasse beau le 7e jour.
Quel est est l’état stable du graphe ?
Que peut-on en conclure ?
L’état stable existe car il n’y a pas de coefficient nul dans la matrice de transition.
Soit 
la matrice correspondant à cet état stable 
.
On a 
et 
soit 
Ce qui nous donne : 
soit 
Soit encore 
Or soit 
.
On a donc : 
Soit 
Conclusion: 
et 
L’état stable est est défini par la matrice : 
ou encore 
On peut donc estimer qu’au bout d’un certain temps il y aura 53% de chance qu’il fasse beau.
Répondre
Want to join the discussion?Feel free to contribute!