Le nombre d’or ou La divine Proportion

Le nombre d’or au centre de cours de mathématique spécial soutien scolaire lycée. Où le trouve-t-on ? Comment effectuer la meilleure approximation ? Lisez nos solutions contenues dans ce cours de soutien scolaire complet…

Vitruve disait…

« Pour qu’un bâtiment soit beau, il doit posséder une symétrie et des proportions parfaites comme celles qu’on trouve dans la nature »

• Dessine un rectangle quelconque, calcule le rapport de la longueur sur la largeur. Recommence plusieurs fois la manipulation.
  Tu dois constater que ce rapport est environ égal à 1,6.
• Mesure ta distance « hauteur totale / distance sol-nombril « et  » ta distance sol-nombril / distance nombril-sommet du crâne » .
  Si les deux rapports sont égaux (environ à 1,6), alors tu es bien proportionné.Ce rapport (1,6) est proche d’un nombre appelé nombre d’or, noté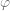 (phi), en hommage au sculpteur grec Phidias (Ve siècle avant J.C.), qui participa à la décoration du Parthénon sur l’Acropole à Athènes

Où rencontre-t-on le nombre d’or ?

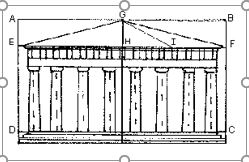Par exemple : le Parthénon s’inscrit dans un rectangle doré, c’est-à-dire tel que le rapport de la longueur à la hauteur est égal au nombre d’or.
Sur la figure ci-contre : .
Sur la toiture du temple,
Le rectangle est appelé rectangle d’or.

Etude mathématique du nombre d’or.

Le nombre d’or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie, comme l’unique rapport  entre deux longueurs  et  telles que le rapport de la somme  des deux longueurs sur la plus grande (), soit égal à celui de la plus grande () sur la plus petite (), c’est-à-dire lorsque : .

Le rapport a/b est alors égal au nombre d’or.

Montrons que ce nombre irrationnel est l’unique solution positive et non nulle de l’équation ou avec

On a :

Soit :

En remplaçant par , on obtient l’équation :

Ou encore par une multiplication des deux membres par (non nul) : soit :

Détermination de la valeur exacte de Phi de façon algébrique :

Niveau classe de seconde

Montrer que :

En déduire une factorisation de (identité remarquable de la forme

Conclure que

Niveau classe de première

Calculer le discriminant du trinôme

En déduire les deux solutions réelles de l’équation  (utiliser les formules et )

Garder la solution positive et conclure que 

Une valeur approchée du nombre d’or est donc 1,618

Lien vers la solution

Une approche par les outils numériques…

Nous allons déterminer une valeur approchée du nombre phi, en utilisant la méthode de dichotomie.

Etant donné f une fonction continue et strictement monotone sur un intervalle [a ; b] telle que f(a) et f(b) soient de signes contraires, l’équation f(x)=0 admet une unique solution dont on peut déterminer un encadrement par dichotomie.

Principe de cette méthode :

• On calcule m le milieu de l’intervalle [a , b].
• Si f(a) et f(m) sont de même signe, c’est que la solution se trouve dans [m ; b] : on affecte à « a » la valeur de m afin de pouvoir continuer le processus.
• Dans le cas contraire, la solution se trouve dans [b ; m] : on affecte à « b » la valeur de m afin de pouvoir continuer le processus.
• On continue le processus jusqu’à obtenir une valeur approchée avec la précision voulue.

Nous allons écrire un algorithme qui met en œuvre ce principe afin d’obtenir une valeur approchée de phi en utilisant les logiciels Algobox et Python, ainsi que les calculatrices (Casio et Texas)

Avec Algobox :
Avec Python :

Avec une calculatrice Casio :

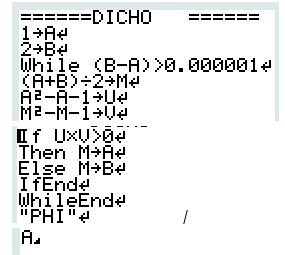Avec une calculatrice Texas Instruments :

En bonus : des méthodes d’approximation du nombre d’or intéressantes !

Une approximation avec des fractions…

est la solution positive de l’équation . En divisant les deux membres de cette équation par (non nul), on obtient .

En remplaçant du dénominateur par l’expression obtenue, on obtient le développement en fraction du nombre d’or :

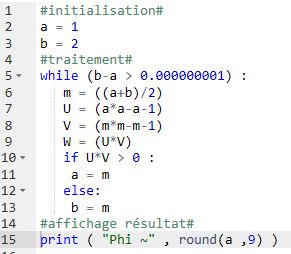
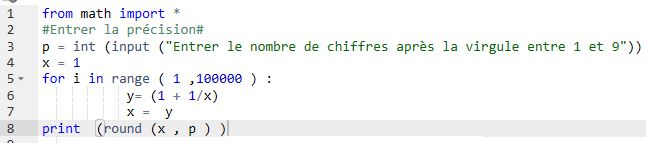
Python permet de calculer une valeur approchée avec cette fraction :

Une autre approximation avec des racines carrées !

est la solution positive de l’équation , donc une valeur positive de s’écrit

Il est possible en remplaçant par cette expression d’obtenir progressivement :

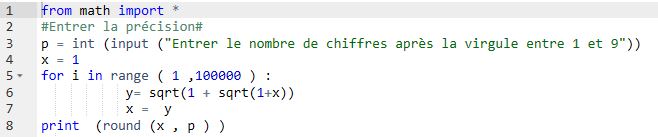
Utilisons cette expression pour obtenir une valeur approchée à l’aide d’un algorithme :

Avec Python :

Et voilà ! grâce à notre émérite E-prof en ligne de soutien scolaire mathématiques, vous savez une grande partie des secrets du mystérieux Nombre d’Or !