Révision bac de mathématiques avec ton e-prof de soutien scolaire en ligne qui te propose ce cours complet sur les matrices.

Ce cours de soutien scolaire en ligne de mathématiques a été préparé pour le niveau TS et TES (Spécialité)
Matrices : Calcul d’un coût de production – Résolution d’un système.
Objectif : Calculer à l’aide d’un calcul matriciel le coût total d’une production de téléviseurs.

Une entreprise fabrique deux types de téléviseurs, téléviseurs HD et téléviseurs 4k.
Pour fabriquer un téléviseur HD il faut 1 unité de bureau d’études, 2 unités de main d’œuvre et 3 unités de composants électroniques.
Pour fabriquer un téléviseurs 4k il faut 2 unités de bureau d’études, 3 unités de main d’œuvre et 6 unités de composants électroniques.
Le coût des unités sont les suivants :
1 unité de bureau d’études coût 45 € ; 1 unité de main d’œuvre coûte 25 € ; 1 unité de composants coûte 30 € .
L’entreprise doit fabriquer 100 téléviseurs HD et 40 téléviseurs 4K.
Déterminons à l’aide d’un calcul matriciel le coût total de cette commande.
On considère les trois matrices :
Matrice A des coûts respectifs d’une unité de bureau d’études, de main d’oeuvre et de composants électronique.
La matrice A est une matrice 1 ligne, 3 colonnes :
Matrice B des quantités, sachant que la 1ere colonne donne les quantités nécessaires en unités de bureau d’étude, de main d’œuvre et de composants électroniques pour un téléviseur HD et la seconde colonne les quantités nécessaires en unités de bureau d’études, de main d’œuvre et de composants pour la fabrication d’un téléviseur 4K.
La matrice B est donc une matrice 3 lignes et 2 colonnes :
Matrice C qui donne le nombre de téléviseurs HD et le nombre de téléviseurs 4K.
La matrice C est une matrice 2 lignes, 1 colonne.
Déterminons de deux manières le coût total de la commande.
1ere manière :
A\times B est la matrice qui donne le coût pour la fabrication d’ un téléviseur HD et d’ un téléviseur 4K.
Le coût total de la fabrication est donc la matrice :
2eme manière :
![]() est la matrice qui donne le nombre d’ unités nécessaires de bureau d’ étude, de main d’ œuvre et de composants électroniques pour la fabrication de 100 téléviseurs HD et de 40 téléviseurs 4K.
est la matrice qui donne le nombre d’ unités nécessaires de bureau d’ étude, de main d’ œuvre et de composants électroniques pour la fabrication de 100 téléviseurs HD et de 40 téléviseurs 4K.
Le coût total de la fabrication est donc la matrice :
Dans les deux cas on trouve que le prix de la fabrication de 100 téléviseurs
HD et de 40 téléviseurs 4K est de 32300 €
Le plus de ton e-prof de soutien scolaire :
Résolution d’un système à l’aide du calcul matriciel.
 Sachant que pour une production quotidienne de x téléviseurs HD et de y téléviseurs 4K l’usine la main-d’œuvre coûte 2025 € et le bureau d’étude
Sachant que pour une production quotidienne de x téléviseurs HD et de y téléviseurs 4K l’usine la main-d’œuvre coûte 2025 € et le bureau d’étude
2000 € ,déterminer en résolvant un système matriciel la fabrication journalière.
En déduire le coût quotidien des composants électronique.
Solution :
x et y sont solutions du système matriciel ![]() .
.
Avec
où :
a = Prix de bureau d’études pour la fabrication d’un téléviseur HD, b celui pour un téléviseur 4K ; c = Prix de la main d’œuvre pour la fabrication d’un téléviseur HD, d celui pour un téléviseur 4K
Ce qui nous donne :
et
On a : ![]()
Soit : ![]()
On obtient à l’aide de la calculatrice :
L’usine fabrique donc quotidiennement 25 téléviseurs HD et 10 téléviseurs 4K.
Ce qui donne un coût quotidien des composants électronique de : ![]() €
€



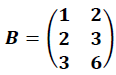

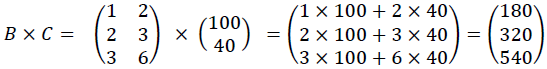
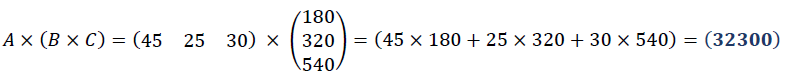
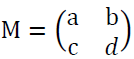


Répondre
Want to join the discussion?Feel free to contribute!