GeoGebra et boîtes de conserve

0 Commentaires

Gérard soutien scolaire mathématiques en ligneLes maths dans la cuisine : si on parlait de boîtes de conserve… C’est ce que propose Gérard, ton E-prof de soutien scolaire en ligne.

Niveau de ce problème de matyhématiques : Bac Pro Terminale ; Lycée 1ere

Prérequis : patron d’un cylindre, représentation graphique, logiciel Géogébra (calcul formel), dérivée, étude de fonction.

GeoGebra et boîtes de conserveSituation : Les boîtes de conserve cylindriques en acier sont fabriquées en découpant des tôles qui sont ensuite recourbées et soudées.

La taille de référence des boîtes est la boîte 4/4.

Sa contenance est de 850 mL, soit 850 cm3, ce qui correspond à une portion pour 4 personnes.

Ta mission: Fabriquer une boîte de conserve cylindrique de taille 4/4, telle que les dimensions de la boîte nécessitent le moins de matière première.

Ceci permettra d’obtenir le coût de production le plus faible possible.

Pour cela il faut que la surface développée de la boîte soit minimale.

Représentons le patron (développement) de la boîte.

exercice de maths sur les boîtes de conserve

Volume d’une boite ayant une hauteur de h cm et un rayon de r cm :  V=\pi \times r^2 \times h

On en déduit : h=\frac{V}{\pi \times r^2} et pour V=850 cm3 on obtient : h= \frac{850}{\pi \times r^2}

Aire S(r) de la boite en fonction de r : S = 2 \times \pi \times r^2 + 2 \times \pi \times r \times h

On remplace h par son expression en fonction de r on obtient :

S=2 \times \pi \times r^2 + 2 \times \pi \times r \times \frac{850}{\pi \times r^2}

Soit encore : S = 2 \times \pi \times r^2 + \frac{1700}{r}

Conjecture : Pour conjecturer la réponse au problème posé, nous allons utiliser le calcul formel du logiciel Geogebra

Voir l’article du blog concernant l’utilisation du calcul formel avec GeoGebra !

Ligne 1 : on entre la fonction , soit S(r) := 2 \times \pi \times r^2 + \frac{1700}{r}

Ligne 2 : on demande au logiciel de déterminer la fonction dérivée,

Ligne 3 : on demande au logiciel de déterminer la valeur du minimum, soit : « Extremum(S(r)) »,

Ligne 4 : on calcule le diamètre correspondant au minimum trouvé,

Ligne 5 : on calcule la valeur de h correspondant.

conjecture avec GeoGebra

On conjecture que pour avoir la surface minimale, il faut que la hauteur de la boîte soit égale à son diamètre.

Fichier Géogébra1

Démonstration en étudiant la fonction

Pour une boîte de volume égal à 850 mL, l’aire peut se calculer à l’aide de la fonction définie par S(r)=2 \pi r^2 + \frac{1700}{r} pour r positif.

Calculons la dérivée de la fonction S par rapport à r et étudions le sens de variation de la fonction pour r positif.

S'(r) = 4 \pi r - \frac{1700}{r^2}

S'(r) = \frac{4 \pi \times 1700 - 1700}{r^2}

S'(r) = 0 si r = \sqrt[3] {\frac {1700}{4 \pi}}=\sqrt[3] {{425}{\pi}} \simeq 5,135

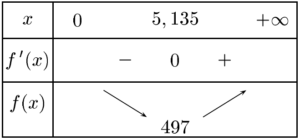
Tableau de variations :

Déterminons enfin la hauteur h de la boîte en fonction de son diamètre d :

h=\frac{850}{\pi r^2} = \frac{2}{r^2} \times \frac{425}{pi}

h=\frac{2}{r^2} \times r^3

Soit : h=2 \times r = d

Conclusion : pour avoir la surface minimale, il faut que la hauteur de la boîte soit égale à son diamètre.

Remarque : cette conclusion est indépendante du volume de la boite

Et pour les casseroles, ça se passe comment ?

Si la casserole a un couvercle, c’est pareil que pour la boîte de conserve.

Mais qu’est-ce que ça change s’il y a un disque de moins dans le calcul de la surface ?
Si la question t’intéresse, tu as tout ce qu’il faut pour refaire les calculs.

Fichier geogebra2

0 réponses

Répondre

Want to join the discussion?
Feel free to contribute!

Laisser un commentaire

Votre adresse de messagerie ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Veuillez répondre à la question suivante *